|
Epsilon 0
E0 or E00 can refer to: * ε0, in mathematics, the smallest member of the epsilon numbers (mathematics), epsilon numbers, a type of ordinal number * ε0, in physics, vacuum permittivity, the absolute dielectric permittivity of classical vacuum * E0 (cipher), a cipher used in the Bluetooth protocol * E0 (robot), a 1986 humanoid robot by Honda * Eo, in electrochemistry, the standard electrode potential, measuring individual potential of a reversible electrode at standard state * E0, the digital carrier for audio, specified in G.703 * E0, Eos Airlines IATA code * E0, ethanol-free gasoline, see REC-90 * e0, in demographics, the life expectancy of an individual at birth (age zero) * E00, Cretinism ICD-10 code * E00, ECO code for certain variations of the Queen's Pawn Game chess opening * ''Enemy Zero'', a 1996 Japanese horror video game for the Sega Saturn See also * 0E (other) {{Letter-Number Combination Disambiguation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Epsilon Numbers (mathematics)
In mathematics, the epsilon numbers are a collection of transfinite numbers whose defining property is that they are fixed points of an exponential map. Consequently, they are not reachable from 0 via a finite series of applications of the chosen exponential map and of "weaker" operations like addition and multiplication. The original epsilon numbers were introduced by Georg Cantor in the context of ordinal arithmetic; they are the ordinal numbers ''ε'' that satisfy the equation :\varepsilon = \omega^\varepsilon, \, in which ω is the smallest infinite ordinal. The least such ordinal is ''ε''0 (pronounced epsilon nought (chiefly British), epsilon naught (chiefly American), or epsilon zero), which can be viewed as the "limit" obtained by transfinite recursion from a sequence of smaller limit ordinals: :\varepsilon_0 = \omega^ = \sup \left\\,, where is the supremum, which is equivalent to set union in the case of the von Neumann representation of ordinals. Larger ordinal ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vacuum Permittivity
Vacuum permittivity, commonly denoted (pronounced "epsilon nought" or "epsilon zero"), is the value of the absolute dielectric permittivity of classical vacuum. It may also be referred to as the permittivity of free space, the electric constant, or the distributed capacitance of the vacuum. It is an ideal (baseline) physical constant. Its CODATA value is: It is a measure of how dense of an electric field is "permitted" to form in response to electric charges and relates the units for electric charge to mechanical quantities such as length and force. For example, the force between two separated electric charges with spherical symmetry (in the vacuum of classical electromagnetism) is given by Coulomb's law: F_\text = \frac \frac Here, ''q''1 and ''q''2 are the charges, ''r'' is the distance between their centres, and the value of the constant fraction 1/(4π''ε''0) is approximately . Likewise, ''ε''0 appears in Maxwell's equations, which describe the properties of electr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
E0 (cipher)
E0 is a stream cipher used in the Bluetooth protocol. It generates a sequence of pseudorandom numbers and combines it with the data using the XOR operator. The key length may vary, but is generally 128 bits. Description At each iteration, E0 generates a bit using four shift registers of differing lengths (25, 31, 33, 39 bits) and two internal states, each 2 bits long. At each clock tick, the registers are shifted and the two states are updated with the current state, the previous state and the values in the shift registers. Four bits are then extracted from the shift registers and added together. The algorithm XORs that sum with the value in the 2-bit register. The first bit of the result is output for the encoding. E0 is divided in three parts: # Payload key generation # Keystream generation # Encoding The setup of the initial state in Bluetooth uses the same structure as the random bit stream generator. We are thus dealing with two combined E0 algorithms. An initial 132-bit st ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
E0 (robot)
The E series was a collection of successive humanoid robots created by the Honda Motor Company between the years of 1986 and 1993. These robots were only experimental, but later evolved into the Honda P series, with Honda eventually amassing the knowledge and experience necessary to create Honda's advanced humanoid robot: ASIMO. The fact that Honda had been developing the robots was kept secret from the public until the announcement of the Honda P2 in 1996. E0, developed in 1986, was the first robot. It walked in a straight line on two feet, in a manner resembling human locomotion, taking around 5 seconds to complete a single step. Quickly engineers realised that in order to walk up slopes, the robot would need to travel faster. The model has 6 degrees of freedom: one in each groin, one in each knee and one in each ankle. Models *E0, developed in 1986. *E1, developed in 1987, was larger than the first and walked at 0.25 km/h. This model and subsequent E-series robots have 12 de ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Standard Electrode Potential
In electrochemistry, standard electrode potential E^\ominus, or E^\ominus_, is the electrode potential (a measure of the reducing power of any element or compound) which the IUPAC "Gold Book" defines as ''"the value of the standard emf ( electromotive force) of a cell in which molecular hydrogen under standard pressure is oxidized to solvated protons at the left-hand electrode"''. Background The basis for an electrochemical cell, such as the galvanic cell, is always a redox reaction which can be broken down into two half-reactions: oxidation at anode (loss of electron) and reduction at cathode (gain of electron). Electricity is produced due to the difference of electric potential between the individual potentials of the two metal electrodes with respect to the electrolyte. Although the overall potential of a cell can be measured, there is no simple way to accurately measure the electrode/electrolyte potentials in isolation. The electric potential also varies with temperat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Eos Airlines
Eos Airlines, Inc. was an American all-business class airline headquartered in Purchase, New York, with its flights from John F. Kennedy International Airport in New York City, New York. On 26 April 2008 Eos Airlines announced its plans to file bankruptcy on its web site, announcing it would cease passenger operations after April 27. History The airline was founded in 2004 by Dave Spurlock, a former director of strategy at British Airways. The company was initially named Atlantic Express and changed its name to Eos in 2005. Eos began operations between New York and London Stansted Airport, London Stansted on October 18, 2005. With the launch of its magazine ''eosCLASS'' in London on 13 March 2008, eos dropped 'Airlines' from its name and altered its slogan to become "eos - Uncrowded. Uncompromising. UNAIRLINE." This change was unveiled by Adam Komack, Chief Lifestyle Officer. Destinations Eos Airlines operated a service between John F. Kennedy International Airport (JFK) and Londo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
REC-90
REC-90 is an ethanol-free, 90 octane unleaded gasoline blend designed for use in recreational/marine engines which can be damaged by the ethanol Ethanol (also called ethyl alcohol, grain alcohol, drinking alcohol, or simply alcohol) is an organic compound with the chemical formula . It is an Alcohol (chemistry), alcohol, with its formula also written as , or EtOH, where Et is the ps ... found in other gasoline blends. It is also usable in some aviation engines and automotive engines, though it has not been thoroughly tested for cars and trucks. Unlike most stations in the plains states which carry ethanol-free 87 octane unleaded alongside 10% ethanol 87 octane unleaded, many states carry ethanol-free gasoline specifically marketed as recreational fuel designed for marine equipment and small engines. Rec-90 Availability and Pricing As debate has ensued over ethanol blending in gasolines, ethanol-free has popped up in a number of states marketed as Rec-90 Recreatio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
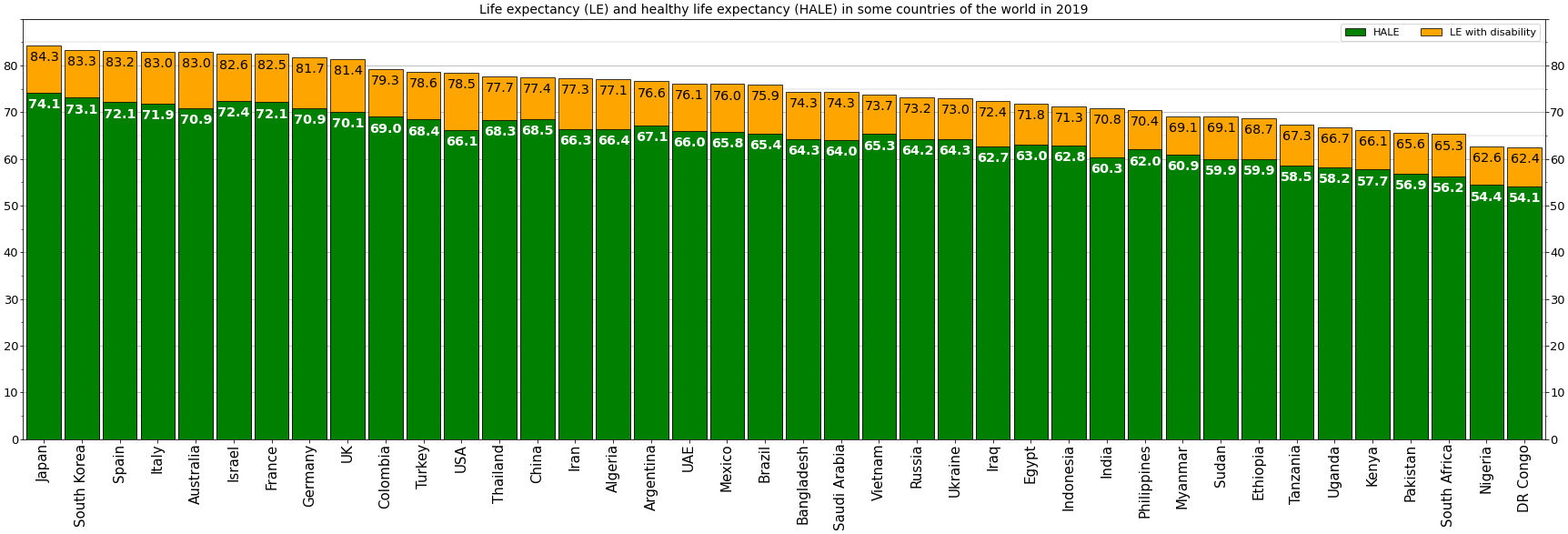
Life Expectancy
Human life expectancy is a statistical measure of the estimate of the average remaining years of life at a given age. The most commonly used measure is ''life expectancy at birth'' (LEB, or in demographic notation ''e''0, where ''e''x denotes the average life remaining at age ''x''). This can be defined in two ways. ''Cohort'' LEB is the mean length of life of a birth Cohort (statistics), cohort (in this case, all individuals born in a given year) and can be computed only for cohorts born so long ago that all their members have died. ''Period'' LEB is the mean length of life of a hypothetical cohort assumed to be exposed, from birth through death, to the mortality rates observed at a given year. National LEB figures reported by national agencies and international organizations for human populations are estimates of ''period'' LEB. Human remains from the early Bronze Age indicate an LEB of 24. In 2019, world LEB was 73.3. A combination of high infant mortality and d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Queen's Pawn Game
The Queen's Pawn Game is any chess opening starting with the move: : 1. d4 It is the second-most popular opening move after 1.e4 (King's Pawn Game). Terminology The term "Queen's Pawn Game" is usually used to describe openings beginning with 1.d4 where White does not play the Queen's Gambit. The most common Queen's Pawn Game openings are: * The London System, 2.Bf4 or 2.Nf3 and 3.Bf4 * The Trompowsky Attack, 1...Nf6 2.Bg5 and the Pseudo-Trompowsky 1...d5 2.Bg5 * The Torre Attack, 2.Nf3 and 3.Bg5 * The Stonewall Attack, 2.e3 * The Colle System, 2.Nf3 and 3.e3 * The King's Fianchetto Opening, 2.Nf3 and 3.g3 * The Barry Attack, 1...Nf6 2.Nf3 g6 3.Nc3 d5 4.Bf4 * The Richter–Veresov Attack, 1...d5 2.Nc3 Nf6 3.Bg5 or 1...Nf6 2.Nc3 d5 3.Bg5 * The Blackmar–Diemer Gambit, 1...d5 2.e4, and the Hübsch Gambit 1...Nf6 2.Nc3 d5 3.e4 In the ''Encyclopaedia of Chess Openings'' (''ECO''), Closed Games (1.d4 d5) are classified under codes D00–D69. Openings where Black do ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Enemy Zero
is a 1996 Horror game, horror-themed adventure video game for the Sega Saturn, developed by Warp (company), Warp and directed by Kenji Eno. Players assume the role of an astronaut who awakens from cryogenic sleep to find her spaceship overrun by invisible creatures who are hunting and killing the ship's crew. They must navigate through the ship in a combination of puzzle-driven exploration rendered in full motion video and first-person shooter sections rendered in real time, during which they must rely on sound to either avoid or kill the invisible enemies. ''Enemy Zero'' was initially designed for Sony's PlayStation (console), PlayStation, but due to grievances with Sony, Eno announced the game would be Saturn exclusive in a dramatic press conference stunt. As support for the Saturn outside of Japan was waning at the time, finding overseas publishers for the game became an uncertain struggle, with Sega itself ultimately taking on publication of the game in both North America and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |